Non-Euclidean and non-metric dissimilarities

Dissimilarities measures may be defined as distances in an Euclidean space or such that they can be interpreted as the Euclidean distances. The Euclidean distances satisfy the triangle inequality: the direct distance between two points is smaller than any detour. They are thereby metric.

Euclidean

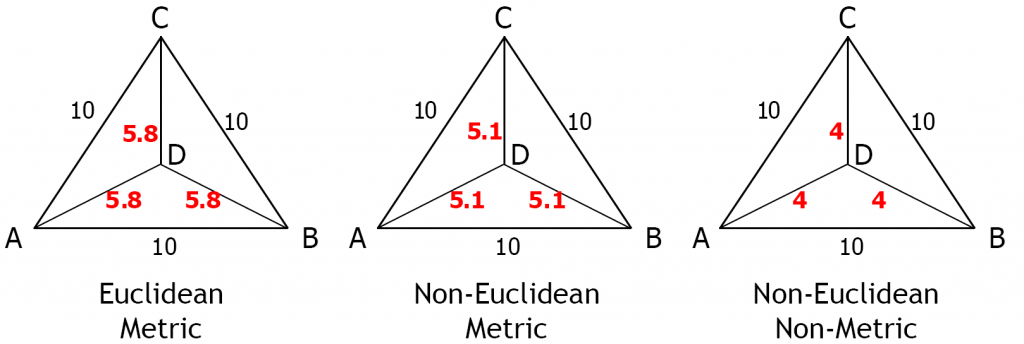
Assume we are given a set of pairwise dissimilarities between four points. For instance, let these be the distances as shown also in the left plot of the example above:

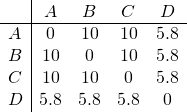
Now we may check whether they can be embedded in an Euclidean space. Yes, indeed, the 2-dimensional configuration is presented in the left plot. This set of distances can thereby be qualified as Euclidean. This set is also metric which can easily be verified by checking all configurations of three points. This is always true for Euclidean dissimilarities.

Non-Euclidean but metric

In the middle plot the dissimilarities are also metric. These are:

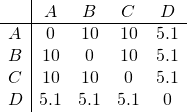
They do not fit, however, to an Euclidean space. It is not possible to find a representation in a two- or higher-dimensional Euclidean space in which the distances between the vectors (points) equal the given pairwise dissimilarities. Consequently, in this example, the dissimilarities are non-Euclidean and metric. It is important to realize that this is possible. In fact it is very common, as often, by definition dissimilarity measures are metric: the dissimilarity between two objects is the smallest difference that can be found according to some optimization procedure. The criteria for such procedures however tend to be non-Euclidean as researchers take into account all aspects of objects that may be relevant. Some may conflict with the Euclidean behavior.

Non-metric

In the right plot, an example is given of a set of pairwise dissimilarities that is non-Euclidean as well as non-metric.

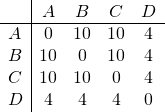
Some criteria and measures are like this, e.g. the Fisher criterion and the Mahalanobis distance between distributions or the modified Hausdorff distance between shapes. In general, non-metric dissimilarities have to be distrusted. There seems to be no guarantee that they make sense in Statistical Learning to constitute a good generalization.

True dissimilarities

However, elsewhere the concept of a true representation has been discussed which may pave the way to a good generalization. The underlying true dissimilarities, dissimilarities that are large for very different objects and small for similar objects can still constitute a non-metric set. Whether a dissimilarity measure is ‘true’ can not formally be checked, but should be verified in the application by an appropriate expert.