The peaking paradox

To measure is to know. Thereby, if we measure more, we know more. This is a fundamental understanding in science, phrased by Kelvin. If we want to know more, or want to increase the accuracy of our knowledge, we should observe more. How to realize this in pattern recognition, however, is a permanently returning problem resulting in a frequently observed paradox..

The paradox …

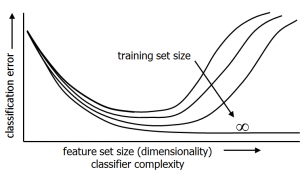
Designers of pattern recognition systems frequently encounter plots as above. They measure more features in order to describe the objects in finer details. This approach may initially help but at some moment it becomes counterproductive. More features increase the complexity of the recognition system. This introduces more parameters to be estimated. The corresponding estimation errors destroy the potentially accessible classification performance. These errors are caused by the limited size of the training set. The solution is thereby to increase this set as well. Only for an infinite training set size holds that the performance is a monotonic function of the number of observations.

… for humans …

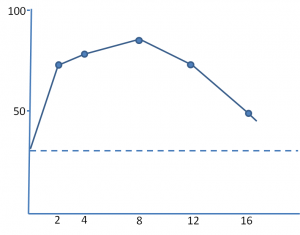It seems to be a paradox: a finer description of the objects by measuring more features can be counterproductive. Is this the result of how we design pattern recognition systems or is it more fundamental? The plot on the right may give a clue. It is based on the recognition accuracy of a set of medical doctors who are given an increasing set of symptoms (2,4, …, 16). They have to make a choice between four possible diseases. First, more information helps, but at some moment the doctors become confused about the incoming information and their good performance deteriorates. (De Dombal, Computer-assisted diagnosis. In: Principles and practice of Medical Computing. 1971, 179).

In this setup, human decision making suffers from the same paradox. This is familiar to anyone who had to undergo some medical examinations in a hospital: don’t make it too extensive, otherwise it will become inconclusive. However, the first time one encounters this phenomenon one is surprised as it does not show up so easily in daily life. In recognizing a face, a voice or a plant the recognition accuracy grows if it is studied longer and in more detail. So what is going on?

… and for computers.

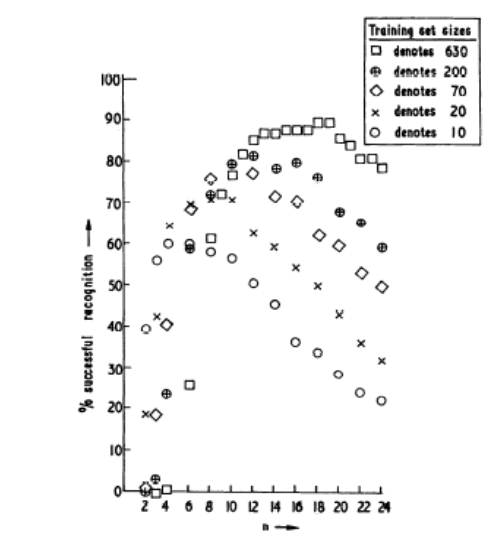The phenomenon has been observed occasionally around 1970 in real world data. An example studied by Ullmann, 1969, is the recognition accuracy of characters based on n-tupels. Increasing the number of n-tuples eventually results in a decreasing performance. Here, it is also observed that more training samples offer a remedy for this phenomenon.

A conclusion might be that more features should go hand in hand with more training data. This is confirmed by various theoretical studies. It corresponds to the statistical phenomenon known as the curse of dimensionality and to Rao’s paradox. However, statistical understanding is in this case not scientific. In the next posts a number of historical attempts will be discussed that aimed to throw more light on the question why the intuitive truth “to measure is to know” should be limited by statistics.