Good recognition is non-metric: true or false?

If the relations between the objects to be recognized are non-metric, there seems to be something wrong. However, Walter Scheirer and his co-authors claim in the  August issue of Pattern Recognition that “Good recognition is non-metric“, [1]:  Is this statement true or false? See also one of the webpages of Walter Scheirer.

Readers of this blog will recognize that the issue of non-metric relation2, or non-Euclidean relations in general, is a frequently returning topic. We found that experts tend to design distance functions between objects in their field of interest that cannot be understood as Euclidean distances between points in a vector space. Moreover, we found that in some applications the non-Euclidean aspect of the data is informative: removing of correcting it deteriorates the recognition performance. See our papers [2] and [3] and the posts of 14 Jan 2013, 21 Jan 2013 and 4 March 2013

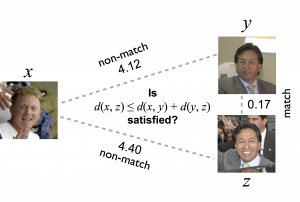The case made in “Good recognition is non-metric“, however, is stronger in several ways. First, the title and the paper deal with nonmetricity: distances between three objects disobey the triangle inequality. In spatial terms, the shortest path between two points is not a straight line, but is found by a detour over a third point. In designing distance measures, people usually try to avoid this, which is usually easy. The result may still be non-Euclidean. For a discussion on the difference between non-metric and non-Euclidean, see a previous post.

Second, the title of the paper suggests that nonmetricity is a condition for a good recognition scheme: if it is good it is non-metric, so if it is metric it is not good. We found, on the contrary, that the vast majority of the publicly available distance based datasets are metric, but are often non-Euclidean, which is weaker, and sometimes even just Euclidean. We never got the idea that recognition based on metric distances is necessarily sub-optimal.

The third issue by which the paper makes a stronger point than our studies is that it is not based on given dissimilarities, but on full recognition systems. It presents a meta-study on published procedures and recognition results and inspects the recognition algorithms with respect to possible non-metric relations. In many multi-class problems tackled by pairwise recognition schemes non-metric relations appeared to arise.

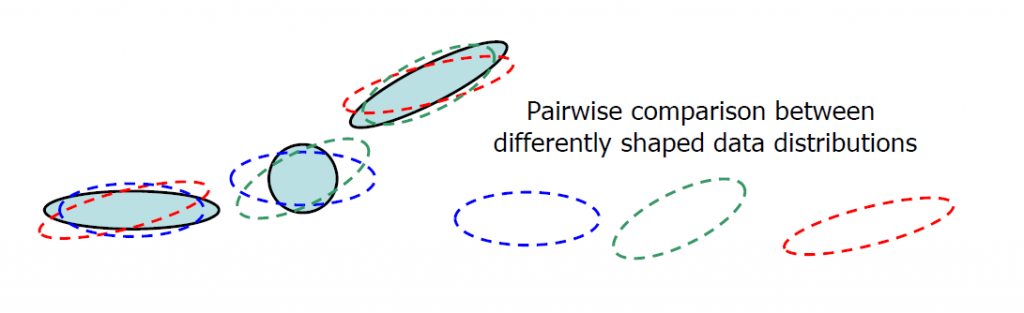We also pointed to this possibility, but never performed a careful study of the literature on this issue. The above picture illustrates how non-metric data may arise in a multi-class problems with different covariance matrices, but assuming equal covariances in a pairwise approach. The left and the middle class compared by the blue averaged covariance, as well as the middle and right class compared by the green covariance have a small distance compared to the much larger distance between the left and right class using the red covariance. The three distances are in fact measured in three different spaces defined by the three pairwise comparisons.

True or false?

Is the provocative statement made by the title true or false? Human recognition starts in a chaotic world in which all objects are judged as completely different. At some moment we see an object that strikes us because of its similarity with a previous one. What is next? Do we use this basis to enlarge the set, using the similar attributes as the main features? Or do we wait for another pair that construct its own basis?

Any group of objects that is considered as a set of similar ones, constructs a context for judging new observations. Different groups generate different contexts. Every object lives thereby in a set of different spaces, depending om the object or class it is compared with. This is the cause of non-Euclidean relations, not necessarily non-metric. The only way to circumvent this is to create a universal context. However, as Walter Scheirer points out, pairwise comparison of classes usually gives better results than a one-against-rest approach in a single context. It depends on the application and the chosen measures whether the non-Euclidean data will include some non-metric examples. This may happen, but it is not a must.

Allowing non-metric relations carries a risk, as the property of compactness might be lost: if all my friends have a common friend who appears to be my enemy, I have a problem. So some type of neighborhood property should be preserved when we allow non-metric relations. This is a point for further investigation.

Conclusion

The title of the paper points into an interesting direction, but seems to be exaggerating. We definitely agree that a good recognition of real world objects may need the use of non-Euclidean relations. These are not necessarily non-metric. There are reasons to avoid nonmetricity. In many approaches, however, this will not harm.

References

1. W.J. Scheirer, M.J. Wilber, M. Eckmann, T.E. Boult: Good recognition is non-metric. Pattern Recognition 47(8), 2014, 2721-2731 (2014)
2. R.P.W. Duin, E. Pekalska, and M. Loog, Non-Euclidean Dissimilarities: Causes, Embedding and Informativeness, in: M. Pelillo (eds.), Similarity-Based Pattern Analysis and Recognition, Advances in Computer Vision and Pattern Recognition, Springer, 2013, 13-44.
3. R.P.W. Duin, Non- Euclidean Problems in Pattern Recognition Related to Human Expert Knowledge, in: J. Filipe, J. Cordeiro (eds.), Enterprise Information Systems, Revised Selected Papers ICEIS 2010, LNBIP, vol. 73, Springer, 2011, 15-28.