Cross-validation

A returning question by students and colleagues is how to define a proper cross-validation: How many folds? Do we need repeats? How to determine the significance?. Here are some considerations.

Why cross-validation?

Cross-validation is a procedure for obtaining an error estimate of trainable system like a classifier. The resulting estimate is specific for the training procedure. There are two main reasons why we want to have such an estimate. First it is used for reporting the expected performance to our customer or project partners when we deliver the classifier. This classifier should be as good as a possible, and so, all available data should be used for training. Consequently there is no separate test set left for an independent evaluation. Cross-validation offers a solution.

A second application is the comparison of different training procedures. The performance itself is not of primary importance here, but the comparison of different procedures by ranking their performances.

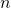-fold cross-validation

Cross-validation solves the problem of delivering a classifier based on all available objects and obtaining an independent estimate of its performance at the same time. This is done by splitting the dataset in parts, in this context called folds. folds are used for training and the fold that has been left out is used for testing. This is repeated times using every fold once for testing. Error estimates are averaged.

At the end all objects are used for testing the classifier which is trained by different objects. So the tests are independent.  The fold classifiers are all trained by a fraction of of the design set. For , every classifier is trained by 90% of the data. It is expected that each of them is almost as good as the final classifier. The error estimate obtained in this way is thereby a little bit pessimistically biased.

It should be realized that just the finite available dataset is used for testing. It has a limited size, otherwise we wouldn’t have a problem. However, if a test set of objects is applied to a classifier with true error the obtained estimate has a standard deviation of .  Whatever further tricks (see below) are included on the -fold cross-validation procedure, it will never get better than that. The uncertainty in the error estimate is fundamentally limited by the finite sample size.

Stratification and density preserving sampling

The finite size of the test set is not the only source of inaccuracy in the error estimate. There are fold classifiers tested and each of them is most likely different from the final classifier that is delivered. Sometimes it is suggested to combine the fold classifiers in one way or the other,. It has, however, to be investigated in what way the obtained cross-validation error based on an average of the errors of the fold classifiers is still an estimate of the error of the combiner.

In contrast to this effort of making use of the diversity of the set of classifiers, some attempts have been made to make the classifiers as equal as possible.  By improving their similarity it is expected that they also become more similar to the final classifier based on the entire design set. The first idea is stratification. By stratified sampling not the design set is sampled to obtain subsets, but the individual classes. This makes the class sizes between the folds more equal. Problems may arise when the classes have very different sizes and some have sizes close to .

One step further is density preserving sampling [4]. This strategy aims to make the probability distributions of the samples in the folds as equal as possible. This will make the classifiers even more alike than by stratification.

Repeated cross-validation

The split in folds by unstratified sampling as well as by stratified sampling is random. If it is repeated a different set of folds is obtained. The resulting classifiers are thereby different which may result in a different error estimate. In order to decrease the inaccuracy caused by the variability of the fold classifiers the entire process may be repeated a number of times. This will stabilize the final result in the sense that the error estimate obtained after times repeated -fold cross validation is expected to change less and less for larger values of .

A stable performance estimate implies that the standard deviation in the average of the  cross-validation estimates shrinks and approximates zero for large . Consequently, differences between the performances of different classifiers become significant for increasing numbers of repetitions . A proper statistical test is not straight forward and should take into account that the classifiers are tested by the same objects, see [3] and [5]. A fast rule of thumb is that the difference between the means of the performances of two procedures is significant if they differ more than the sum of the estimated standard deviations of the performances in a single -fold cross-validation.

Repeated cross-validation removes the variability in the obtained error estimate. This estimate, however, is still a prediction of the performance of the final classifier based on the entire design set. This prediction has a standard deviation of at least as explained above. Repeating the cross validation will not remove this uncertainty as long as it is based on the same set of objects.

Popular procedures

The most popular cross-validation procedures are the following:

1. 10-fold cross-validation, as followed from a study by Kohavi [1]. This became very popular and has become a standard procedure in many papers.
2. 10 times 10-fold cross-validation. This may be useful for comparing classifiers as the 10 repeats shrink the standard deviations in the means of the estimated classifier errors.
3. 5 times 2-fold cross-validation as proposed by Dietterich [2]. In this paper it is shown how to compute the significance of differences in classification error means. This is later improved by Alpaydin [3].
4. 8-fold density preserving sampling as proposed by Budka and Gabrys [4]. The number of folds in this procedure should be a power of 2. Repeating makes no difference as the sampling is deterministic.
5. Leave-one-out (LOO) cross-validation. In this case the number of folds is equal to the number of objects in the design set ( 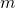above). For large datasets this is very time-consuming. The sampling procedure is deterministic as simply all folds of 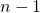objects are considered. So repeating makes no difference.

The first four of these are compared in a large experiment in which every procedure is applied to seven classifiers. The cross-validation error predictions are compared with the performances of the classifiers based on the entire design set. This results, for every procedure, in a difference between the estimated ranking of seven classifiers (based on the cross-validation of the design set) and the true ranking (based on the performance of the classifier trained on the full design set and estimated on a large, independent test set). It appeared that 10 times 10-fold cross-validation has usually to be preferred and that 8-fold density preserving sampling is never significantly worse. but is much faster. The full experiment (in Matlab) may be downloaded.

References