Never use the test set for training. It is meant for independent validation of the training result. If it has been somewhere included in the training stage it is not independent anymore and the evaluation result will be positively biased.
This has been my guideline for a long time. Some students were shocked when I started to experiment in the opposite direction, partially triggered by the literature. Why to do it differently? Does the above not hold?
Training the final classifier
The first, very good reason has been recognized all the time. At some moment, after analyzing a dataset extensively, a final classifier has to be delivered. From various train set – test set splits and cross-validation experiments it has already to be clear what performance can be reached. The classifier to be delivered to the customer or supervisor should be as good as possible and so it has to be trained by all data that is available. There is no data left for testing but previous results obtained from a part of the dataset may give a fair estimate. The final classifier might be slightly better than our estimate, but in practice it may even be worse if the analysis took many rounds in which train set and test set have been used repeatedly.
Semi-supervised learning
There is a second reason to use the test set for training. Every object to be classified brings its own information about the problem at hand. This is most clear for high-dimensional problems given by a small dataset. Additional objects can be helpful to determine a relevant subspace with a higher accuracy, e.g. by principal component analysis. The true labels of test objects that are included in such an analysis should not be used, of course. In this way a better classifier may be found, which can still be evaluated by the same test set, now using its labels. This has to be paid by a repeated training for every (set of) test object(s) to which the procedure has to be applied. There is no final classifier that can directly be used. Depending on the new test objects, a new classifier has to be computed.
Such a procedure can be called transductive learning. There is no induction, as there is no classifier computed to be applied to all future objects. Instead, a classifier has been derived that should be applied to just the objects at hand. Here is an example.
Example
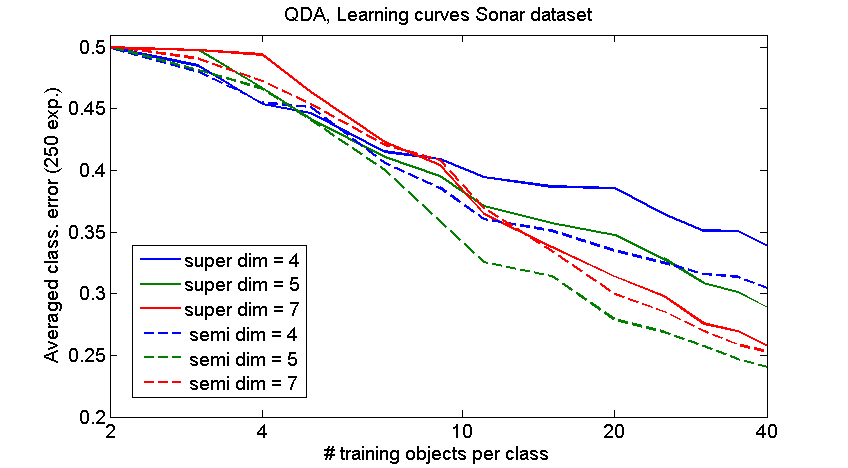The figure shows the result of an experiment using the quadratic classifier QDA on the Sonar dataset. This two-class dataset has 208 objects in 60 dimensions. Small training sets of 2 to 40 objects per class are used. All other objects, without their labels, are added to the training set to compute, by PCA, low-dimensional subspaces of 4, 5 or 7 dimensions. In these subspaces the labeled training set only is used for computing a classifier which is applied to all test objects. The resulting classification errors are shown in the vertical direction. Classification errors for small training sets are very noisy. For that reason the average over 250 (!) repetitions are shown. In each run the dataset was randomly split into a training set of the desired size and a test set.
Conclusion
The results might seem promising. The use of the test set for building an appropriate feature reduction needed for the small training set sizes is of significant help. However, the following points have to be considered before a final judgment on the applicability should be made.
- It took some effort to find an example like this. Several datasets, classifiers and subspace dimensionalities had to be examined.
- Training sets should be small, but not very small, in order to profit from an additional unlabeled set. If there is no performance, it cannot be improved. Also nothing can be gained in case of sufficiently large training sets.
- A single additional object is hardly of any help. The additional unlabeled set should preferably an order larger than the labeled set.
- Additional unlabeled set might be counterproductive. If use for linear feature extraction, like in the above example, the extracted subspace might be bad for the small training set.
As an additional unlabeled set may improve as well deteriorate the result a cross-validation procedure is needed to determine whether it should be used or not. However, usually it might only be helpful for small training sets, cross-validation results may not be significant for a final judgement. Given this state of affairs, research focuses on procedures that will certainly not hurt.
Filed under: Classification • Evaluation
