Features need statistics, as they reduce

Is statistics needed for learning? Well, it depends. A definite answer will be postponed for the time being. Here a first step will be made based on the traditional representation used for pattern recognition: the feature space.

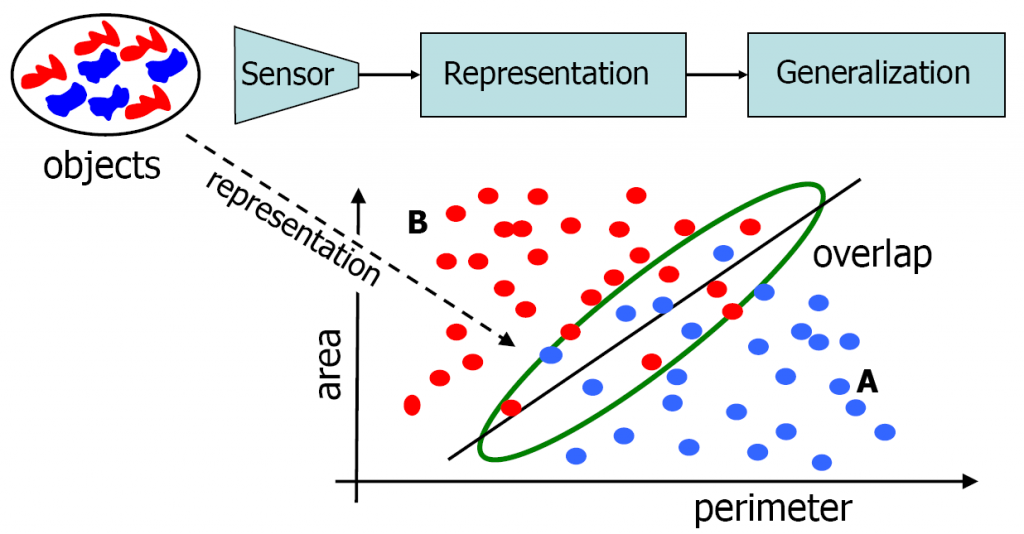
Objects belonging to different pattern classes differ. Otherwise it would not be possible to distinguish these classes. May be the differences can be described by a small set of specific properties. If they are small for objects in the same class and significant for objects in different classes they are useful as features. Objects can be represented by points (vectors) in a feature space. An example for a two-class problem is shown in the figure.

Classes overlap

The two features perform reasonably well for this problem. Classes are compact and there is a somewhat empty space between them. There is however an area for which the two classes overlap. Any classifier constructed by a simple smooth decision boundary, e.g. linear or quadratic, will make errors. This holds for this given training set and it is to be expected that the classification error for new objects to be classified by this function will at least as large.

In order to minimize the error in the area of class overlap it is needed to obtain a good estimate of the probability density function in this area. So it is needed to use a statistical analysis to obtain such estimates. Unless there is some prior knowledge on the distributions, which is not very common, density estimates have to be based on a training set that is representative for the objects to be classified in future. Otherwise a classifier will not be optimal for these objects. The best way to obtain such a representative set, in fact the only way if no additional knowledge is available, is to select a random set of objects (i.i.d) out of the set of objects to be classified in future.

Statistics are needed

Consequently, a statistical analysis is needed if the object representations for different classes overlap. Why in fact do they overlap? Why is it that there are points in the feature space that represent objects from one class as well as from another class? It might be that there are objects that are ambiguous w.r.t. there class membership. For instance, if we want to distinguish the handwritten digits ‘1’ and ‘7’ then sometimes a digit might be encountered that may belong to both classes.

Feature representations reduce

A much more common cause of class overlap is however that the feature representation does not cover a full object description. There might be object differences that are not expressed in features, e.g. they may differ in weight or colour while the features just describe shape and size. For almost any real world object a finite set of features will not describe the entire object. Some object differences are not reflected by feature differences and occasionally this may happen for objects of different classes. The result is that classes overlap in feature space.

In summary, as the feature representation reduces, classes overlap and statistics are needed to handle the overlap region. Proper probability density estimates are needed for this and they demand that classes are sampled in a statistical representative way. This is bad as it demands large sets of objects.

This approach is entirely different from human learning. If we want to teach to a child the difference between goats and sheep, we show it typical examples characterizing the class differences well.  In addition we may add a few examples that are close to the class borders. There is no need at all to sample the entire classes of goats and sheep in a statistical way. This will cause many similar examples that are not helpful at all to grasp the class difference.