How should I interpret the output of a classifier?

PRTools distinguishes two types of classifiers: density based and distance based. Some classifiers follow a slightly different concept but are squeezed into these two types.

Density based classifiers

Density based classifiers estimate for every class a probability density function f_i(\textbf{x}) in which i is the class and \textbf{x} the vector representing an object to be classified. Classification can be done by weighting the densities by the class priors p_i:

F_i(\textbf{x}) = p_i f_i(\textbf{x})

and selecting the class with the highest weighted density:

c_{\textbf{x}} = \mathrm{argmax}_i(F_i(\textbf{x}))

Sometimes we want to use posterior probabilities (numbers in the [0,1] interval) instead of weighted densities ([0,\infty)). They just differ by normalization:

P_i(\textbf{x}) = F_i(\textbf{x}) / \sum_j(F_j(\textbf{x}))

They result into the same class assignments

c_{\textbf{x}} = \mathrm{argmax}_i(P_i(\textbf{x})) = \mathrm{argmax}_i(F_i(\textbf{x})/ \sum_j(F_j(\textbf{x})) = \mathrm{argmax}_i(F_i(\textbf{x}))

as the normalization factor sum_j(F_j(\textbf{x}) is independent of i. Here is a PRTools example based on the classifier qdc which assumes normal densities. The routine classc takes care of normalization;

a = gendatd;       % generate two normal distributions
[test,train] = gendat(a,[2 2]); % 2 test objects per class
w = qdc(train);    % train the classifier
F = test*w;        % weighted densities of the test objects
+F, % show them
0.0005    0.0000
0.0062    0.0004
0.0000    0.0078
0.0000    0.0075
P = test*w*classc;  % compute posterior probabilities
+P, % show them
0.9887    0.0113
0.9415    0.0585
0.0020    0.9980
0.0014    0.9986

After computing F or P the class labels assigned for the test objects can be found by

F*labeld % Generates the same result as for P*labeld
1
1
2
2

Distance based classifiers

Distance based classifiers assign class labels on the basis of distances to objects or separation boundaries. Densities and thereby posterior probabilities are not involved. In order to find a confidence measure comparable to posterior probabilities, PRTools transforms for the distance d(\textbf{x}) to the separation boundary (which are in the interval ((-\infty,\infty)) by a sigmoid function to the interval (0,1). Distances are scaled before the sigmoid is taken by a maximum-likelihood approach: the likelihood over the training set used for the classifier is optimized. Classifier conditional posteriors are obtained for two classes A and B by using the optimized sigmoid and one minus this sigmoid.

S(\textbf{x},\alpha ) = \mathrm{sigmoid}(\alpha : d(\textbf{x}))

\hat{\alpha} = \mathrm{argmax}_\alpha (\prod_{j \in A} (S(\textbf{x}_j,\alpha)) \prod_{j \in B} (1-S(\textbf{x}_j,\alpha)))

P_A(\textbf{x}) = S(\textbf{x},\hat{\alpha} ), P_B(\textbf{x}) = 1-S(\textbf{x},\hat{\alpha} )

See also our paper on this topic (Classifier conditional posterior probabilities, SSSPR 1998, 611-619). This approach is followed for all classifiers that optimize a separation boundary like fisherc, svc and loglc. Multi-class problems are solved in by a one-class-against-rest procedures (mclassc)  that results in a confidence for every class.

By applying the inverse sigmoid function invsigm posterior probabilities computed in the above way can be transformed backwardly into distances. It has to be realized, however, that these distance are not the Euclidean distances in the given vector space but that they are scaled in the above way.

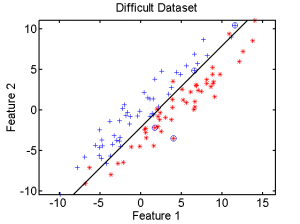
a = gendatd; % generate two normal distributions
[test,train] = gendat(a,[2 2]); % select 2 test objects per class
scatterd(a); % scatterplot of all data
hold on; scatterd(test,'o'); % mark test objects
w = fisherc(a); % compute a classifier
plotc(w); % plot it
d = test*w; % classify test objects
+d % show posteriors
0.8920    0.1080
0.6929    0.3071
0.0220    0.9780
0.0000    1.0000
+(d*invsigm) % show scaled distances
2.1110   -2.1110
0.8137   -0.8137
-3.7946    3.7946
-11.4872   11.4872

Other classifiers

There are various other classifiers that do not fit naturally in the above scheme, e.g. as they compute distances to objects that cannot be negative. Here it is shortly indicated for some of them how they are squeezed in the above concept.

  • The one-nearest-neighbor classifier knnc([],1) uses the distances to the first neighbor of all classes. The sigmoid of the logarithm of the sum of these distance divided by the individual distance for a particular class is used as an estimate for the posterior probability. This is followed by a normalization to guarantee that the sum of the posteriors over all classes is one for every object that is classified.
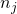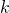  • All other nearest neighbor classifiers estimate directly posteriors by the counting the numbers of objects n_j for all c classes in a neighborhood of k objects. Bayes estimators are used: P_j(x) = (n_j+1)/(k+c).
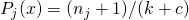  • The nearest mean classifier nmc uses postulated spherical Gaussian densities around the means and computes posteriors from that assuming that all classes have the same prior.
  • The scaled nearest mean classifier nmsc is a density based classifier that assumes spherical Gaussian densities after scaling the axes. It is thereby equivalent to udc.
  • Neural network classifiers like lmnc, bpxnc, rbnc and rnnc use the normalized outputs as posteriors.
  • Decision trees such as treec and dtc use the same Bayes estimators like knnc over the number of training objects found in their end nodes.
Print Friendly, PDF & Email