PRTools, elements, operations, user commands, introductory examples, advanced examples

Datasets

On this page the dataset is introduced. It is one of the key elements of PRTools

• Background
• Definition, constructor, label list, label type
• Overload
• Structure
• Examples

Dataset background

The dataset is a PRTools variable type in which the vector representation of a set of objects is stored together with object class labels, class priors, and other useful annotation of the objects, the measurements or the dataset in its entirety. The vector elements traditionally correspond to features, but may also refer to pixel values in an image, spectral intensities for a set of wavelengths, amplitudes of a time signal at given points in time, dissimilarities with a fixed set of other objects, etcetera. Essential is that every object the same set measurement values are available.

The core of a dataset is a data matrix of m rows (corresponding to the objects) and k columns (corresponding to the measurements). The columns are usually referred to as features but they may have another background as in the above examples. A dataset is hereby an enriched version of a data matrix.It has a size of m*k and many of the Matlab operations for matrices apply. In addition PRTools adds specific dataset operations and, most important, the large set of routines for dimension reduction, classification, evaluation and visualization know how to handle datasets. This avoids that users have to manipulate additional parameters and annotation themselves.

Dataset definition

Constructor

The class of dataset variables is called prdataset. In the past it was just, natually, dataset, but this was changed in PRTools5 to avoid clashes with other toolboxes.

The prdataset constructor looks like

a = prdataset(data,labels)

• data is an array of size [m,k] storing the k-dimensional vector representations of m objects.
• labels contains the m object labels. The following types are supported:
  – numeric: a columns vector of k integers (users are discouraged to use this type).
  – strings: a character array ok k strings.
  – cells: a 1-dimensional vector of k cells, each containing a string.

The two items data and labels are essential for the operation of PRTools. If data is neglected (data = []) an empty dataset is defined. If labels is not supplied the objects remain unlabeled. In case just a part of the objects have no labels the corresponding entry of labels should contain a NaN for numeric labels or an empty string ('') in case of string labels.

The label list (class names)

In order to speed up the handling of labels they are stored in a (character) array of class names (called lablist). Instead of dealing with the possibly long names, PRTools just uses for every object an index (called nlab) into lablist. For more information see the description of the prdataset structure and the commands for storing information into a dataset and retrieving it.

Label types

There are three types of labels supported for datasets:

• crisp. These are the traditional nominal class labels, either integer numbers or strings (class names). Object can belong to just a single class.
• soft. These labels are real values interval [0,1]. For every class a value has to be specified, not necessarily summing to one. They may be interpreted as fuzzy memberships, as class confidences or as posterior class probabilities.
• targets. These are numeric values on the interval (-infinity,infinity). Every object has for every class a target. This facility enables the construction of routines for multiple regression within the PRTools framework. There are just a few routines that use this facility.

Dataset overload

Although datasets may carry various kinds of additional information, they can be treated like 2-dimensional matrices in many common Matlab constructs. See the section dataset operations for examples. The resulting datasets always have, as far as applicable, the same fields as the original dataset. Where needed they are adapted (e.g. sizes and labels) to assure that the result is a consistent dataset.

Dataset structure

Various items can be stored in a dataset. A full list can be found be converting a dataset variable into a structure.

data = rand(6,2);
labels = [1 1 1, 2 2 2]';
a = prdataset(data,labels)
% 6 by 2 dataset with 2 classes: [3 3]
struct(a)
%
% data: [6x2 double]
% lablist: {2x4 cell}
% nlab: [6x1 double]
% labtype: 'crisp'
% targets: []
% featlab: []
% featdom: {}
% prior: []
% cost: []
% objsize: 6
% featsize: 2
% ident: [1x1 struct]
% version: {[1x1 struct] '03-Jan-2011 15:24:04'}
% name: []
% user: []

All fields have a corresponding set-command (e.g. setdata) to store it and a get-command (e.g. getdata) to retrieve it. Users are discouraged to use the ‘.’-constructs (e.g. a.files) as it will not guarantee consistency with other fields. In some cases not the exact fields are retrieved but some derived data. In the table more information is given.

When datasets are changed, e.g. by a transformation of the data, or by taking a subset of features or objects, all relevant information is copied, including the name and user field.

See the commands for the dataset definition and multi-labeling for more information on how to access the fields

Examples

Below some examples are given of dataset manipulations. Use is made of the PRTools command genlab(N) that generates a set of numeric labels, N(i) for class i. The command scatterd is similar but not identical to the Matlab command scatter and has thereby a similar, slightly different name.

% delete all figure
delfigs

% reset random seed for repeatability
% randreset(1)

% Generate in 2 dimensions 3 normally distributed classes
% of 20 objects for each class
a = prdataset(randn(60,2),genlab([20 20 20]))
% 60 by 2 dataset with 3 classes: [20 20 20]

% Give the features a name
a = setfeatlab(a,char('size','intensity'))
% 60 by 2 dataset with 3 classes: [20 20 20]

% Make the distributions of the classes different and plot them
a(1:20,:) = a(1:20,:)*0.5;
a(21:40,1) = a(21:40,1)+4;
a(41:60,2) = a(41:60,2)+4;
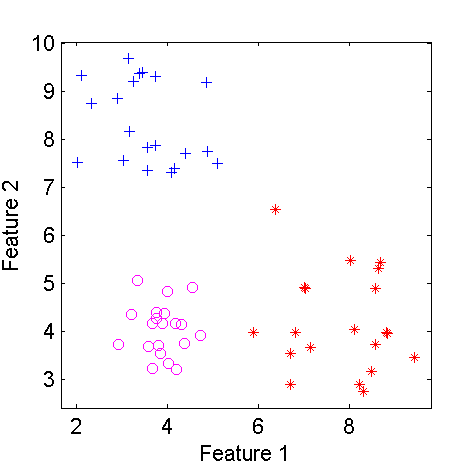
figure; scatterd(a)

% create a subset of the second class
b = a(21:40,:)
% 20 by 2 dataset with 3 classes: [0 20 0]

% add 4 to the second feature of this class
b(:,2) = b(:,2) + 4*ones(20,1)
% 20 by 2 dataset with 3 classes: [0 20 0]
% concatenate this set to the original dataset
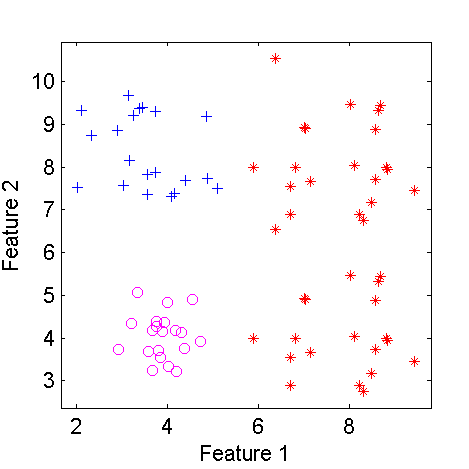
c = [a;b]
% 80 by 2 dataset with 3 classes: [20 40 20]
figure; scatterd(c);
showfigs

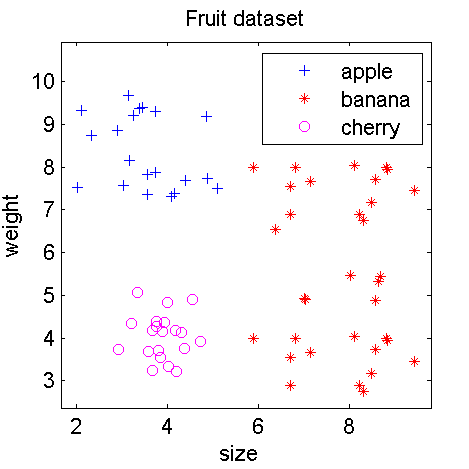
For better annotation of the plot we may add some information on the dataset, the classes and features in some recognizable way, e.g.

c = setname(c,'Fruit dataset');
c = setlablist(c,char('apple','banana','cherry'));
c = setfeatlab(c,char('size','weight'));
figure; scatterd(c)

The annotated dataset

elements: datasets datafiles cells and doubles mappings classifiers mapping types.
operations: datasets datafiles cells and doubles mappings classifiers stacked parallel sequential dyadic.
user commands: datasets representation classifiers evaluation clustering examples support routines.
introductory examples: Introduction Scatterplots Datasets Datafiles Mappings Classifiers Evaluation Learning curves Feature curves Dimension reduction Combining classifiers Dissimilarities.
advanced examples.