Why is the nearest neighbor rule so good?

Just compare the the new observations with the ones stored in memory. Take the most similar one and use its label. What is wrong with that? It is simple, intuitive, implementation is straightforward (everybody will get the same result), there is no training involved and it has asymptotically a very nice guaranteed performance, the Cover and Hart bound.

The nearest neighbor (NN) rule is perhaps the oldest classification rule, much older than Fisher’s LDA (1936), which is according to many is the natural standard. Marcello Pelillo dates it back to Alhazen (965 – 1040), which is not fully accurate as Alhazen described template matching as he had no way to store the observed past, see a previous post. Anyway, it has a long history, has interesting properties, but it is not very popular in machine learning studies. Moreover, iIt was neglected for a long time in the neural network community. Why is that?

Is it that researchers judge its most remarkable feature, no training, as a drawback? May be, may be not, but for sure, this property positions the rule outside many studies. It is very common in machine learning to describe statistical learning in terms of an optimization problem. This implies the postulation of a criterion and a way to minimize it. Some rules are directly defined in this way, e.g. the support vector classifier. Other rules can be reformulated as such. However, the NN rule is not based on a criterion and there is no optimization. It directly relies on the data and a given distance measure.

One way to judge classifiers is by their complexity. Intuitively this can be understood as the flexibility of shaping the classifier in the vector space during the above optimization procedure. Complexity should be in line with the size of the dataset to avoid overtraining. The VC complexity of the NN rule, however, is infinite. According to the statistical learning theory this is very dangerous. It will result in a zero-error empirical error (on the training set), by which here is the danger of an almost random result in classifying test sets. We are warned: do not use such rules. And yes, artificial examples can be constructed that shows this for the NN rule.

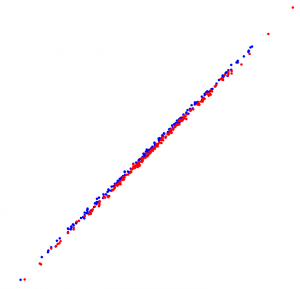On the left, 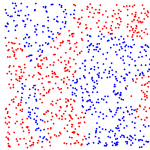a 2D scatter plot of almost separable classes for which the NN rule performs badly. The distances of nearest neighbors of different classes are similar to those of the same class. There exists, however, a linear classifier that separates the classes well. The scatter plot on the right shows classes for which the NN rule performs reasonably well. For this case advanced classifiers like a neural network or a non-linear support vector classifier are needed to obtain a similar result..

Here is a key point. High complexity classifiers are dangerous as they can adjust the decision boundary in a very flexible way that adapts to the given training set, but does not generalize. This also holds for the NN rule. However, the performance of that rule can very be easily estimated by a leave-one-out cross-validation. As there is no training needed it is as fast as computing the apparent error (which will be zero) . On the other hand, estimating the leave-one-out error for other high-complexity classifiers can be computationally very expensive as retraining is needed. Moreover, the estimated performance should ideally be included in the training procedure, which is prohibitive. Consequently, the danger that comes with a high complexity is not present for the NN rule. It can be safely applied after judging the leave-one-out error.

It might be argued that the NN rule does not perform a proper generalization, as it just stores the data. The generalization is in the given distance measure. This might be true, but almost all classifiers depend in one way or the other on a given distance measure. Next, the size of the storage might be criticized. Accepted, but some neural networks store a comparable collection of weights and need considerable training.

Again, why is the NN rule so good in spite of its high complexity? There is the following evolutionary argument. Problems for which nearest neighbors have different labels will not be considered. They are directly neglected as wrongly formulated or too difficult. Recognition problems arise in a human context, in scientific research or in applications in which human decision making has to be supported. Thereby, they can directly, after looking at a few examples, be considered as too difficult. They will be put aside and the effort will be focused into another direction.

The NN neighbor rule is good as it reflects human decision making because it is based only a distance measure designed or accepted by the analyst. Secondly, and most prominently, because no training is needed just problems will survive for further investigation in which this rule shows a promising result. In short, the NN rule is good because it matches the problems of interest and vice versa.