Is every pattern recognition problem a small sample size problem?

If we want to learn a new concept we may ask for a definition. This might be good in mathematics, but in real life it is often better to get some examples. Let us, for instance, try to understand what despair means. The dictionary tells us that it means ‘loss of hope’. This is just rephrasing. We didn’t learn anything new if we already know the words ‘loss’ and ‘hope’.

Human learning from examples

In order to learn something new, some examples are needed instead of a definition. Asking the internet for related paintings produces very soon the famous Scream by Munch. You may also ask for some music and find Mahler 10. In literature, of course, much can be found, e.g. in the novels of John Steinbeck, as well as in his biography.

How many real world examples do we need to understand what despair means? The first picture is already very helpful, and after listening to some pieces of music and reading a few short stories or (parts of) some novels we may have a good understanding of the concept. Is it possible to feed a pattern recognition system with the same small set pictures, music and texts such that it will recognize similar real world examples of the occurrence of ‘despair’? This might be doubted.

Automatic learning from examples

It is more realistic to expect that thousands of real world, observable expressions of despair are needed and perhaps a set of complicated neural networks to have any success. We are dealing with a complex concept which cannot easily be learned from a few examples. So may be for humans, having the experience of life, this can be done, but for training a pattern recognition system not having this context, thousands or many more examples will be needed.

Is  this not true for many more problems, even for seemingly simple ones like character recognition? This application could only be solved after large training sets became available as well as computers to handle them. So not just for complex concepts, but also for simple ones, large datasets may be needed.

The small sample size problem

In the daily pattern recognition practice still many problems arise, e.g. in medical applications in which just a few tens of objects are available. The collection of more examples is very expensive or virtually impossible. These are truly small sample size problems. The study of the general aspects of such problems has generated many papers handling overtraining and the curse of dimensionality. See the 1991 paper by Jain and Raudys for a classic study.

Overtraining happens if the complexity of the system we have chosen for training is too large for the given dataset. Consequently the system will adapt to the noise instead of to the class differences. The solution is either to enlarge the dataset, but, if not possible, to simplify the system. A big problem is, however, that in practice we do not know whether overtraining happens, unless a sufficiently large test set is available. If we would have it, it would be better to add it to the training set as this will generally improve the classifier. Consequently, the optimal complexity of the system cannot be determined and has to be chosen blindly. Of course, past experience and prior studies will be very helpful to make an appropriate choise.

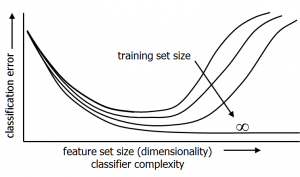Overtraining might not be a problem for a large training sets. However, the classifier complexity can always be enlarged, e.g. by a higher non-linearity, or by more layers or units in a neural network. This will cause a more detailed description of the dataset.  Initially, a better classification performance can be expected, but by increasing the complexity too far, the system may start to suffer from overtraining again.

This may be phrased again as having a small sample size problem: the dataset is too small for the chosen complexity of the model. The problem of adapting the complexity of the generalization procedure (dimension, number of parameters, regularization) to the given dataset size will always arise in the attempt to optimize the classification performance. In this sense, every pattern recognition problem has to face the small sample size problem in searching for the best performance.