The Pixel Space

As image pixels are used for computing features, the pixel representation seems to be more general. This has the advantage limitations caused by that bad or missing features  can be overcome by a thorough  analysis of the pixel space. There is however a price to pay.

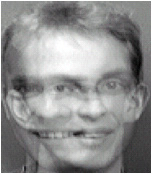
Consider two face images represented by their pixels. In the pixel space the two images can be averaged. The result is shown above in the middle image. This image however does not show a face. There are four eyes and two noses. The average of two faces brings us outside the domain of faces. The picture on the right illustrates an explanation. In the high dimensional pixel space (it has about 25000 dimensions as the images have a size of 170 x 150)  the line between two remote images goes through a large region of images that do not represent faces. Just very close to the original images it may contain faces.

The collection of faces in the pixel space is a non-convex subspace. For most frontal faces it is fully connected as can be observed from an example set on YouTube, e.g. a selection of Rembrandt’s self-portraits. Any image between the two shows a proper face proving that there is an unbroken path of pixel representations of proper faces.

A similar phenomenon even holds for simple images like digitized handwritten numerals. Images of 32 x 32 pixels constitute a 1024 dimensional space. The set of handwritten ‘7’- s however does not constitute a cloud in 1024 dimensions. A study of the number of degrees of freedom makes this clear. A ‘7’ can be written in 5 to 10 strokes. Every stroke has a starting point and an end point. As most of these strokes are connected, each of them contributes thereby with at most 4 degrees of freedom. So a handwritten ‘7’ has less than 20 degrees of freedom. The set of all ‘7 constitutes a subspace of less then 20 dimensions. This subspace is concave and thereby non-linear as interpolations of many pairs will not generate another ‘7’.

In conclusion, classes in a pixel space may not construct a convex cloud. They are thereby not normally distributed and classification schemes based on assuming normal densities will not be optimal. Also linear classifiers will be sub-optimal as the non-linear subspaces describing such classes need more advanced classification procedures.