Statistical pattern recognition

Statistical pattern recognition refers to the use of statistics to learn from examples. It means to collect observations, study and digest them in order to infer general rules or concepts that can be applied to new, unseen observations. How should this be done in an automatic way? What tools are needed?

Previous discussions on prior knowledge and Plato and Aristotle make clear that learning from observations is impossible when context is missing. Context information should be available for learning to occur! Why? Because, otherwise, we don’t know where to look for or how define meaningful patterns.Without the reference to the context, there is no way to derive a single general statement on the observations, because many of them are equally possible. Context is necessary to make a choice.

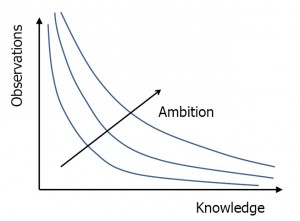There is a trade-off between how much knowledge that we already have and the number of observations that is needed to gain some specific additional insight. It is shown in the figure on the right. If we know everything no new observations are needed. The less we know in advance the more examples are needed to reach a specific target. This all depends on how ambitious we are in reaching a specific goal.

Discussions like this are very symbolic. Knowledge does not have a size that can be measured. It can at most be ranked partially: from a specific starting point it can grow. Information theory might be helpful when we accept that knowledge can be expressed in bits of information. This implies always an uncertainty. Prior knowledge however usually comes as certain.  The expert cannot estimate how convinced he is that he is right. The medical doctor who tells us what to measure where, or what are clear examples of a disease cannot tell what the probability is that this is correct. Moreover, in daily life, we may be absolutely certain after a finite number of observations: we meet somebody and within a second we are sure it is our neighbor. This does not fit in an information theoretic approach.

This is again an aspect of the struggle to learn from examples. Prior knowledge might be wrong, but is is the foundation for new knowledge. For the time being we solve this dilemma by converting existing knowledge into facts of where we are sure of and unknowns between them that have to be uncovered. In the so-called Bayesian approaches it is assumed that some prior probability for the unknowns are known, for sure (!?). The next step in any learning approach, Bayesian or not,  is now to bring the known facts, the observations and the unknowns in the same framework, in some mathematical description, by which they can be related. This is called representation.

On the basis of the representation the observations can be related. The pattern recognition task is to generalize these relations to rules that should hold for new observations outside the set of the given ones. The entire process of representation and generalization is illustrated by the below figure. There are some real world objects. The given knowledge is that they come in two different, distinguishable classes, the red ones and the blue ones. It is also given that their size (area) and perimeter length are important for distinguishing them. Examples are given The rule to distinguish them is unknown. It should be found such that it can be applied to new observation for which the class is unknown and has to be estimated.

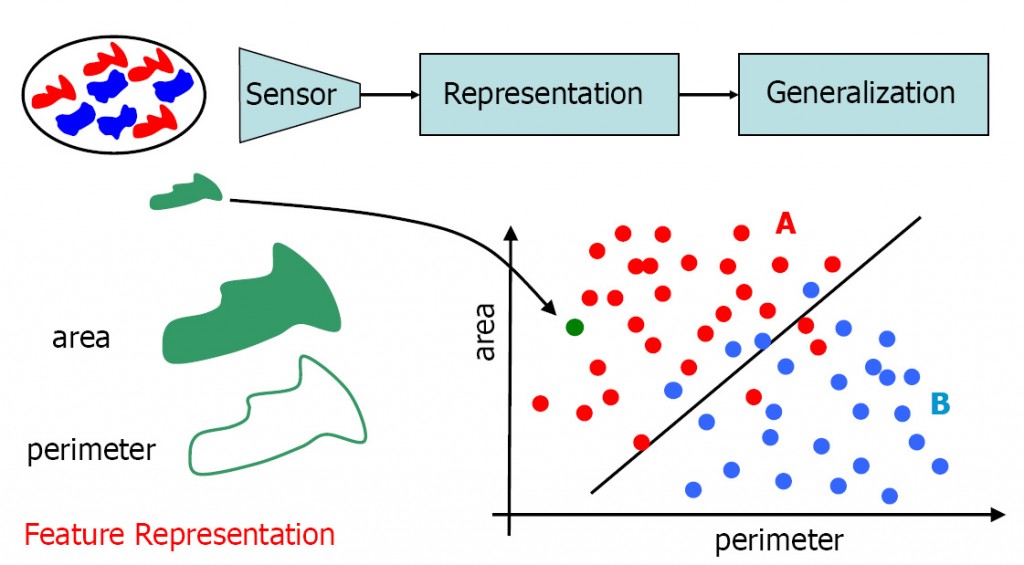The objects are represented in a 2-dimensional vector space. Every object is represented as a point (a vector) in this space. It appears that the training examples of the two classes are represented in almost separable regions in this space. A straight line may serve as a decision boundary. It may be applied to new objects with unknown class membership to estimate the class they belong to.

In this example still some training objects go wrong. So it is to be expected that the classification rule is not perfect and that it will make errors for future examples. The main target in the development of a pattern recognition system is to make this error, as small as possible. Additional targets may be the minimization of the cost of learning and classification. To achieve these targets we need to study:

1. representation: the way the objects are related, in this case by a 2-dimensional vector space.
2. generalization: the rules and concepts that can be derived from the given representation of the set of examples.
3. evaluation: accurate and trustworthy estimates of the performance of the system.